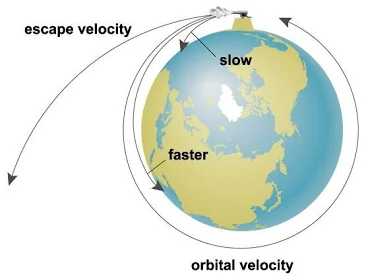
Imagine you are sitting on a skateboard at the bottom of your drive and you need to get to the top.

You could push off your garage door and if you pushed hard enough, you could make it to the top of the drive. This initial push, the speed required to just make it to the top is your escape velocity.

Or you could stand up and skate to the top.

This is is what the rocket is doing. It doesn’t need a big initial speed as it’s got constant propulsion.

In fact, as long as it’s got enough thrust to overcome the force of gravity, it could creep up out of the Earth’s gravity well at skateboard pace.

But this would use a ridiculous amount of rocket fuel. Which would make the rocket even heavier, and therefore require even more fuel, making it even heavier…

So it gets up and out as quickly as possible, as this is the most fuel efficient.

If you had to use escape velocity to launch people into space, the initial acceleration required would liquify them, the vehicle would travel 11.2 km in the first second! But it would have to accelerate to this speed in a lot less than this distance, so a lot less than a second.

Even if you had a launch device that was a kilometre long, taller than the tallest buildings on Earth, this would mean reaching Mach 1 in the first 30 m and Mach 33 by the time you leave the top, an acceleration of 6,400 g, over 100 times a fatal acceleration.

So we use rockets instead.

I’m quite surprised that the only solution the other answers gave to your pseudo-paradox is that you are confusing orbiting and escaping.

But let me reassure you : a rocket does not need to reach this insanely high escape velocity to escape from Earth’s gravitational field !

Let me try to answer that with almost no maths :

Simply because the escape velocity is calculated at a given distance from the center of mass of a system. It just tells you how fast an object needs to be at a certain distance from the center of mass to escape : just give it such a speed and you needn’t do anything else (i.e. no thrust).

The calculation of escape velocity relies on the fact that the only force that applies to the escaping object is its weight (gravity). But in the case of a rocket, the thrust is not just initial, it keeps applying all along the ascent so the simple “escape velocity” calculation isn’t really relevant (it’s not a projectile, it’s a system that has thrust all along its escape).

For just a teeny bit of maths (oui … c’est inevitable !) and to make it more convincing, you have the following :

v=√2GMR+hv=2GMR+h

Where vv is the escape velocity at altitude hh .

So it follows that the escape velocity is divided by √22 when you reach an altitude equal to the radius of the earth. When you reach h=3R≈19000kmh=3R≈19000km then the new escape velocity is only half what it was at the surface, so just 1200012000 mph ! If you manage to get the rocket that far at this new, more reasonable escape velocity, then you can cut off the thrusters