There is an obvious answer and a super, amazingly cool one.

The obvious one is that in the vacuum of space, there is nothing to block the light – and photons don’t “decay” or anything – so it goes on forever.

The cool answer lies in special relativity.

You know that special relativity says that the faster something goes – the slower its clocks tick as seen by an outside observer…right?

Well it’s not only time that’s distorted – the length of an object moving at high speed contracts along the direction it’s travelling.

If you switch perspective and imagine that you’re inside a spaceship moving at close to the the speed of light – then you can’t tell that you’re being slowed down and contracted – instead, it looks to you as if the outside world is being speeded up and squashed along the direction you’re moving.

These effects get more and more pronounced the closer you get to the speed of light.

When you actually HIT the speed of light – the universe is shrunk to an infinitely thin disk that you’re passing through at right angles – and time in the rest of the universe is going INFINITELY fast.

So from the perspective of a photon – all of the places it’s going are squashed together into a point – and all of time happens in less than the blink of an eye…the universe goes from Big Bang to ultimate death in zero time!

So for the photon – it is simultaneously at all points along its journey and it takes zero time to get there.

It doesn’t have time to decay – and it’s already at its destination the moment it starts.

“Absorber theory” says that light literally cannot be emitted UNLESS it “knows” that it is going to be absorbed. Absorber theory was the first substantial piece of work done by Richard Feynman, with John Wheeler.

Maxwell’s equations of light are symmetric in time — they show waves going backward and forward in time. Physicists disregard the wave solution showing light going backward in time. We don’t hear radio broadcasts from the future, do we? So obviously these solutions are “unphysical”. When I studied physics, the lecturer literally wiped the “time reversed” solution off the chalkboard to eliminate it.

There was a physicist called Hans Tetrode who had a similar idea, which really intrigued Einstein. Tetrode said, light from a star would not reach your eye, if your eye was not there to receive it.

I have studied this question of “time-reversed” waves for decades now, it’s fascinating. At school, we were taught about Huyghens’s secondary wavelets. We drew a circular, expanding wavefront, and then took each point on that wavefront as a new point source of circular waves.

If you do this, you get an expanding wavefront going outward, and a contracting wavefront going inward. But our physics textbook at school insisted that this ingoing wave somehow “cancelled”, if you did the calculations properly.

When I got to university, I found that by “cancelled”, they meant rubbing it off the chalkboard and pretending the inward-moving wave did not exist because it was “unphysical”.

Go and look. There is absolutely no such calculation showing that the “inward” wave cancels. Sometimes an absolutely arbitrary factor is introduced, with an angular dependence, that goes to zero for the inward wave. This is a straight fudge. If anyone can produce a proper calculation showing that the inward wave disappears, I’ll be very interested.

As other answers to this question have pointed out: for a photon, there is no time at all between emission and absorption. Literally, emission and absorption are one unified event from the photon’s point of view. The best way of expressing this is Roger Penrose’s twistor theory. In twistor theory, a light ray going from A to B is replaced by a point, which “squashes” A exactly on top of B. This is actually what the photon experiences. Again, the emission and absorption are one single event for the photon.

If the universe is expanding forever, as many physicists think, then all light will not be absorbed. Absorber theory seems to have faded into the background. However, the closer you look at quantum field theory, the more you see “operators” operating backward in time to keep the scheme consistent.

To get a “real” probability distribution out of quantum theory, you have to multiply the wave function by its complex conjugate. Now, in relativity theory, the imaginary part of spacetime is time: it is multiplied by i, the square root of negative one. Therefore, when you take the complex conjugate, you actually reverse the time direction. You can see this in “bra-ket” notation: <Y| and |Y> have arrows pointing in different directions, it’s actually time that is reversed.

So every time you “prepare” a real physical state in quantum mechanics, by doing this complex conjugation of the wave function, you are taking a wave from the future and combining it with a wave from the past, to calculate the state in the present moment.

And “the present moment” is all there is in quantum physics. There is no actual time variable in quantum mechanics, only instantaneous snapshots. You cannot tell what happened in the past or what will happen in the future, from the wave equations of QM. You can only deduce probabilities about the past and the future.

Feynman once took Maxwell’s equations and showed someone that you could derive the quantum wave function from them (I’ll have to find that one again, I think it’s in Gleick’s biography). So Maxwell’s equations presaged both relativity and QM. Maxwell’s equations are worth taking really seriously.

They have been tinkered with in various ways, but the worst offence is the blanket denial of the existence of the ingoing wave. It’s real, and you can see it even in water waves. Next time you see a slow-motion drop of water hitting a pond, and a “rebound” droplet bouncing upward, you are actually seeing the influence of the ingoing wave, forcing the water upward.

As Feynman pointed out: the ingoing wave passes through the centre, the origin of the wave, and carries on travelling on the other side. I call it the “in-gone” wave; after it passes through the centre, it rides exactly on top of the outgoing wave you see in the pond. Absorber theory shows this: the ingoing and outgoing waves exactly coincide with each other. You can see it in this diagram:

Here, the time-reversed waves are called “advanced waves”, meaning actually that the emitter is advanced in time and the waves are sent backward in time. “Retarded” waves actually mean the emitter is retarded and sends waves forward in time, the way we usually understand the situation.

You see the advanced and retarded waves cancel exactly before the emission and after the absorption, respectively. They coincide exactly in between emission and absorption, this is what I mean by the two waves riding together.

There is one absolute condition for absorber theory to work, which is why it is called absorber theory: light MUST be absorbed, in order for it to be emitted. And again, the moment of emission and absorption is identical for the photon itself. It literally takes two different, perhaps widely separated points in spacetime, and makes a single unified event out of them. Spooky action at a distance is right there in Maxwell’s equations, if you look.

In fact, this is just Newton’s Third Law. If body A exerts a force on body B of any kind—mechanical, electrical, magnetic, gravitational—then body B exerts an equal, but opposite force on body A. And this happens instantaneously.

So: electron A emits a photon that travels and hits electron B and gives it a “kick”. Electron A feels a “recoil” kick at the moment of emission. According to absorber theory, that “kick” has come from electron B, via a wave travelling backward in time. So spooky action at a distance is actually right there in Newton’s laws, if you’re brave enough to look.

My money is on absorber theory to make a comeback, it’s time this gerrymandering of Maxwell’s equations was fixed. And one day, any kid at school should be able to tell you: light will never travel forever. It only got emitted because it “knew” it was going to be absorbed in the future. A star only shines light at you—as Tetrode maintained—because it “knows” you are there in the future, waiting to see it.

There is actually a way in which “absorber theory” can work without an absorber, and light can therefore theoretically travel forever. I saw this argument somewhere and managed to blank it entirely from my mind, until I worked it out again for myself recently while trying to see how “negative events” that are unobservable can occur. This forgetfulness was a real case of confirmation bias on my part, I regret to say, I should have mentioned this formulation earlier.

However: I then managed to work out a counterargument that may just work to preserve the time symmetry of solutions to Maxwell’s equations. In the interests of completeness, please bear with me while I go through this.

Remember that the goal here is to find solutions to Maxwell’s equations that are truly symmetric in time. If you have darkness followed by light that travels forever, you have a fundamentally asymmetric solution, so the following argument really bothered me — I really can’t remember where I saw this, I’d be grateful if someone can remind me.

The first issue is this: if we take Maxwell’s equations to be symmetric in time, then an emitter will send waves travelling both forward into the future and backward into the past. The way this is represented generally looks as follows, with the emitter experiencing a recoil “kick” at the moment of emission:

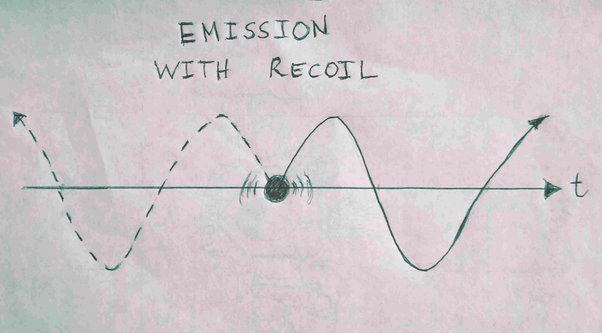
Here the solid line represents the wave going forward into the future (the so-called “retarded” wave, with the emitter behind the wave in time) and the dashed line represents the wave going backward into the past (the “advanced” wave, with the emitter ahead of the wave in time). Note that these waves are mirror-symmetric around the moment of emission; this is what we expect from a time-symmetric solution to Maxwell’s equations. So far, so good.

If there is no absorber on either side, then we just have light on both sides of the emission — light travelling forever in both directions. This is a symmetric solution, which is what we’re looking for. If this simple picture were to hold, then we would see light and hear radio signals coming to us from the future. We don’t experience these phenomena, so there must be more to the situation.

Let’s accept, then, that there was a Big Bang or a singularity back in the past from which the Universe emerged, as modern cosmology insists; and let’s see what happens if there is no Big Crunch up ahead, and the photon we are tracking manages to miss all the matter in the Universe, doesn’t get absorbed by a black hole or anything else, and just carries on forever; while the light travelling backwards hits and is absorbed (or is otherwise nullified) by the singularity at the very beginning of time itself.

The singularity achieves this by negating the backward-travelling wave with a forward-travelling wave, as indicated by the solid red line below.

This wave then carries on past the original emission, only it now reinforces the emitted wave. This is the situation we then get, the picture which I blanked out of my mind:

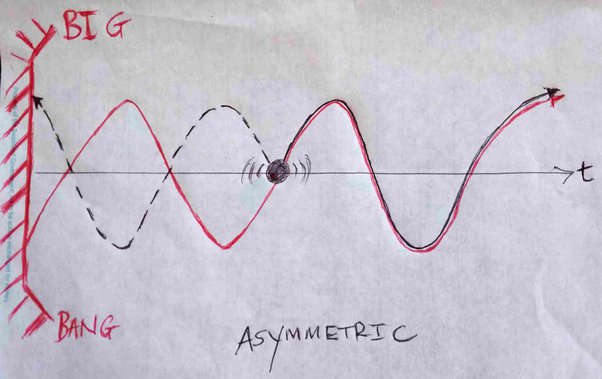
Because of the asymmetry of the Universe — a Big Bang on one side, but no Big Crunch on the other — we thus get a fundamentally asymmetric solution. No light is seen before the emission (so we don’t hear radio signals from the future, in line with our ordinary understanding of causality), but we do have light travelling forever after the emission.

So this scenario might be taken as an answer to the question: how can light travel forever? We have a fundamentally asymmetric, unbalanced solution here: no light, followed by light. This arises from the symmetry of Maxwell’s equations being projected into an asymmetric Universe.

In looking at this picture, I started thinking about the issue of “radiation resistance”, represented by the recoil that an electron experiences as it emits a photon. In absorber theory, that recoil kick comes from the absorber, sending back a wave in time, as I originally described above. This is just Newton’s third law: if body A exerts a force on body B, then body B exerts an equal but opposite force on body A.

If there is no absorber up ahead, no body B, then there is no wave travelling backwards, and therefore there will be no recoil kick experienced by the emitter. There will be no radiation resistance at all. If you push against a wall, the wall will push back on you; but if you push against nothing at all, you will just fall forward and continue falling.

This absence of a radiation recoil will — surely — affect the advanced wave that the emitter sends backward in time. I therefore put the following scenario to you. Because there is no recoil of the emitter, the advanced wave sent into the past is now just an extension of the retarded wave the emitter is sending into the future, it’s all one continuous wave:

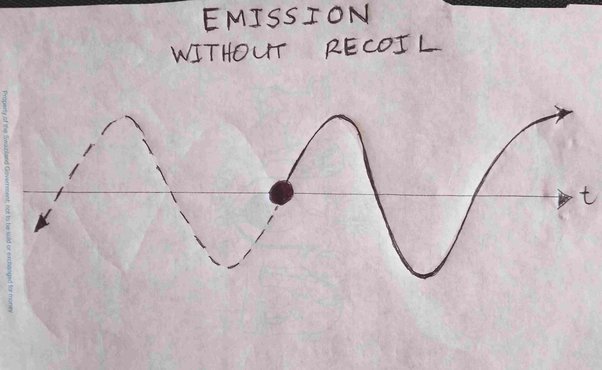
Assume now that there is indeed a Big Bang in the past, which cancels this advanced wave. We then get the following picture:

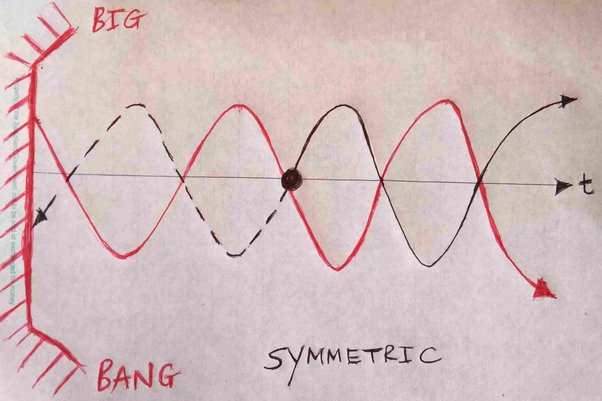
This, now, is a truly symmetric solution to the situation. We have no light before the emission, and we also have no light after the emission either: the Big Bang acts to cancel the entire event. Nothing whatsoever will be seen, including no observed recoil of the emitter, although “something” definitely happened.

This is my best guess, then, given the Big Bang, for what constitutes a true “negative event” that is completely unobservable: the Universe’s origin acts to cancel light when there is no absorber up ahead, i.e. when there is no observer to see it.

To be honest, I am not at all convinced that there was a Big Bang in the way cosmologists describe it. For me, every single emission of light is a “little bang”, and it can only occur if there is an absorber up ahead to act as a “little crunch”, to preserve the time symmetry of Maxwell’s equations.

Since every single photon follows this pattern, the combination of all this light may indeed create the impression that there was a “big bang” back there, from which the Universe emerged, while experiments with antennas and radiation resistance seem to indicate that all radiation is somehow absorbed ahead in time, giving the appearance of a “big crunch” — whatever value astronomers may obtain for Hubble’s constant (which is surely a variable, anyway), or whatever dark energy may seem to be doing in making the Universe expand forever.

However, for the first time, I can actually see some real utility to the Big Bang, in acting to nullify “disallowed” emissions in directions where there is no absorber, no observer up ahead to see the light.

I’m sorry to have complicated the picture, but this really is my best shot at producing truly symmetric solutions to Maxwell’s equations, even if the Universe is fundamentally asymmetric in having an apparent beginning, but no apparent end. If you try to shine a light in a direction where it cannot be absorbed, that “apparent beginning”, or Big Bang if you prefer, will act to nullify the entire event.

If you count this as a “negative event”, then you can very simply calculate negative probabilities corresponding to states that cannot be observed; and these negative probabilities are a fact within quantum mechanics, whether you like it or not.